String Theory, Higher Dimensions, and the Theory of the Universe
|
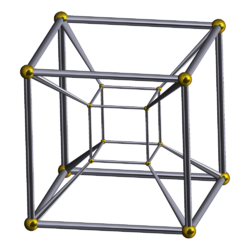
| This is a tesseract. This object lives in the 4th spatial dimension.
A single dot lives in the zero dimension; a line lives in the 1st dimension; a square in 2D; a cube in 3D;
and a tesseract is 4th dimensional.
|
|
The Strong Nuclear Force bonds quarks together inside protons, neutrons, and other hadrons
|
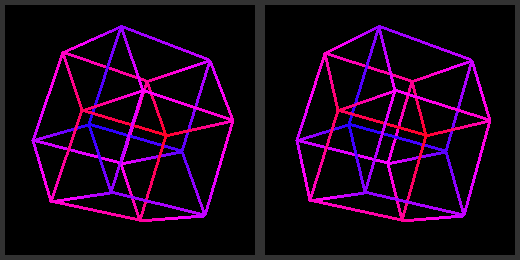
| This is the rotating shadow of a tesseract, rotating along a single axis.
|

|
Bosons are particles with an integer spin, as opposed to fermions which have half-integer spin.
|
| 3D tesseract challenge: stare at the center of the picture,
slowly cross you eyes until the images merge into 1; it will pop into the 3rd dimention!
|
|
| The heterotic string has two types of vibrations, clockwise and counterclockwise.
Clockwise vibrations live in 10-dimensional space; counter-clockwise vibrations are in 26-dimensional space.
Higher dimensions have a symmetry (like curved space), and the vibrations in these higher dimensions assume the same symmetry.
"The symmetries of the subatomic realm are but remnants of the symmetry of highter-dimensional space," says physicist Michio Kaku.
"Perturbation theory only works if space–time has some rather otherworldly properties, one of which is supersymmetry. While the strings in the initial hadronic theory were bosonic (i.e. their vibrations corresponded to particles such as photons that have integer values of spin in units of Planck's constant), the world is mostly made up of fermions – particles such as electrons and protons, which have half-integer spins. In the mid-1970s Schwarz and others realized that the only way string theory could accommodate fermions was if every bosonic string vibration has a supersymmetric fermionic counterpart, which corresponds to a particle with exactly the same mass (and vice versa). String theory is thus shorthand for superstring theory." -
source: physicsworld
|

|
The other demand that string theory places on space–time is a seemingly ridiculous number of dimensions. The original bosonic theory, for example, only respects Lorentz invariance – an observed symmetry of space–time that states there is no preferred direction in space – if it is formulated in 26 dimensions. Superstrings require a more modest 10 dimensions: nine of space and one of time. But in order to explain the fact that there are only three spatial dimensions, string theorists have to find ways to deal with the additional six, which is usually done by "compactifying" the extra dimensions at very small scales.
|



